STARK-Friendly Hash Challenge

Published on 03 Feb 2020

In this post, I discuss the STARK-Friendly Hash Challenge, a competition with the goal of finding collisions for several hash functions designed specifically for zero-knowledge proofs (ZKP) and multiparty computations (MPC). I managed to find collisions for 3 instances of 91-bit hash functions using the classic parallel collision search method with distinguished points from van Oorshot and Wiener [vOW99]. This is a general attack on hash functions and thus does not exhibit any particular weakness of the chosen hash functions. The crucial part is to optimize the implementations to make the attack cost realistic, and I will describe some (common) arithmetic tricks in this post.

A pdf version of this note is available at orbilu.uni.lu

Full implementation code is available at github.com/cryptolu/starkware_hash_challenge

The Challenge

The goal of the challenge is find a concrete collision pair for one of the proposed hash instances. The challenge covers four families of recently proposed hash functions:

HadesMiMC: Starkad and Poseidon (2019, Grassi et al.)
MARVELlous: Vision and Rescue (2019, Aly et al.)
GMiMC (2019, Albrecht et al.)
MiMCHash-2q/p (2016, Albrecht et al.)

All considered families are based on the Sponge construction for hash-functions. The only differences are in the parameters: the underlying permutation $f$, the rate $r$ and the capacity $c$.

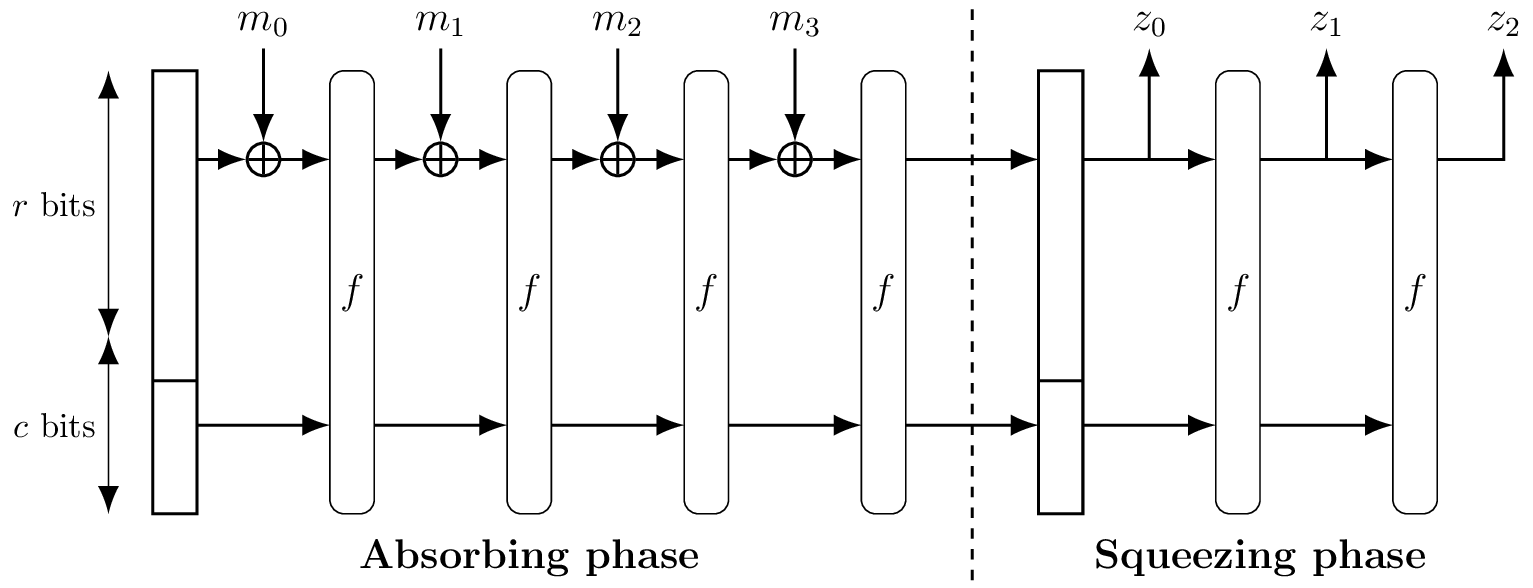
Figure: The Sponge construction (credits: [Jea16])

Under the assumption of "secure" permutation $f$, a sponge is provably secure up to $c/2$ bits. According to this bound, the challenge organizers proposed multiple concrete instances of hash functions with expected security of 45 bits, 80 bits, 128 bits, and 256 bits.

Low Security Instances

One could expect that 45 bits can be broken very fast. Indeed, the 56-bit DES key space can be exhaustively checked by a single modern GPU in under a month. There is a caveat: the security is measured in evaluations of the attacked function. 45-bit security therefore means that about $2^{45}$ such evaluations are required to attack the primitive. In order to mount a generic attack as fast as possible, the attacker has to optimize the implementation of the primitive itself.

The target hash functions are designed to be efficient in the ZKP/MPC settings, meaning that they are mainly optimized to have a small number of multiplications in the chosen finite field. The primitives use binary or prime fields, with size ranging from 64 to 256 bits. Arithmetics in these fields are not natural for common architectures, and thus are quite inefficient on practice.

Medium+ Security Instances

With 80+ bits of security, generic attacks are infeasible: a novel practical cryptanalytic attack has to be developed. Is it realistic to expect it? Note that the competition lasts less than a year.

On one hand, symmetric cryptography based on arithmetics over large finite fields (especially prime fields) is a rather new direction and is not well studied. Indeed, a new cryptanalytic technique might be discovered for such primitives. Furthermore, the primitives themselves are rather recent.

On the other hand, there are several arguments against such attacks.

The first argument is that the proposed targets use full number of rounds, which are quite large by design in order to protect against interpolation/algebraic attacks.

The second argument is the use of the sponge construction. The sponge significantly limits the attack surface:

The SHA-3 standard (Keccak) pessimistically uses a permutation with 24 rounds, while after some effort at most 8 rounds are attacked by completely infeasible attacks. The designers proposed a hash function using the same permutation reduced to 12 rounds [BDP+18], and there were even proposals to reduce it to 10 rounds [Aum19].
Recently, another competition on practical cryptanalysis of a sponge-based hash function held: Troika Challenge. Various rewards were proposed for practical collision or preimage attacks for amounts of rounds varying from 1 to 12 (while the primitive itself uses 24!). After a year, only the 3-round version was broken with a collision attack and the 2-round version was broken with a preimage attack.
Some variants of MiMC/GMiMC block ciphers are vulnerable to birthday-bound attacks [Bon19], i.e. their security is effectively halved. This happens because these variants are equivalent to an Even-Mansour cipher: a key-less permutation with a key addition only before and after the permutation. However, in the sponge mode this is not useful: the cipher is used as a permutation anyway!

Summary

To sum up, the most realistic targets are only those with 45-bit security. The main part of this post will also suggest that even for those targets the required amount of computations is quite unreasonable.

Parallel Collision Search

The main algorithm is the generic parallel collision search [vOW99]. The trick to parallelize the search without using too much memory is to track only distinguished points - hash values with e.g. a particular number of leftmost bits equal to zero.

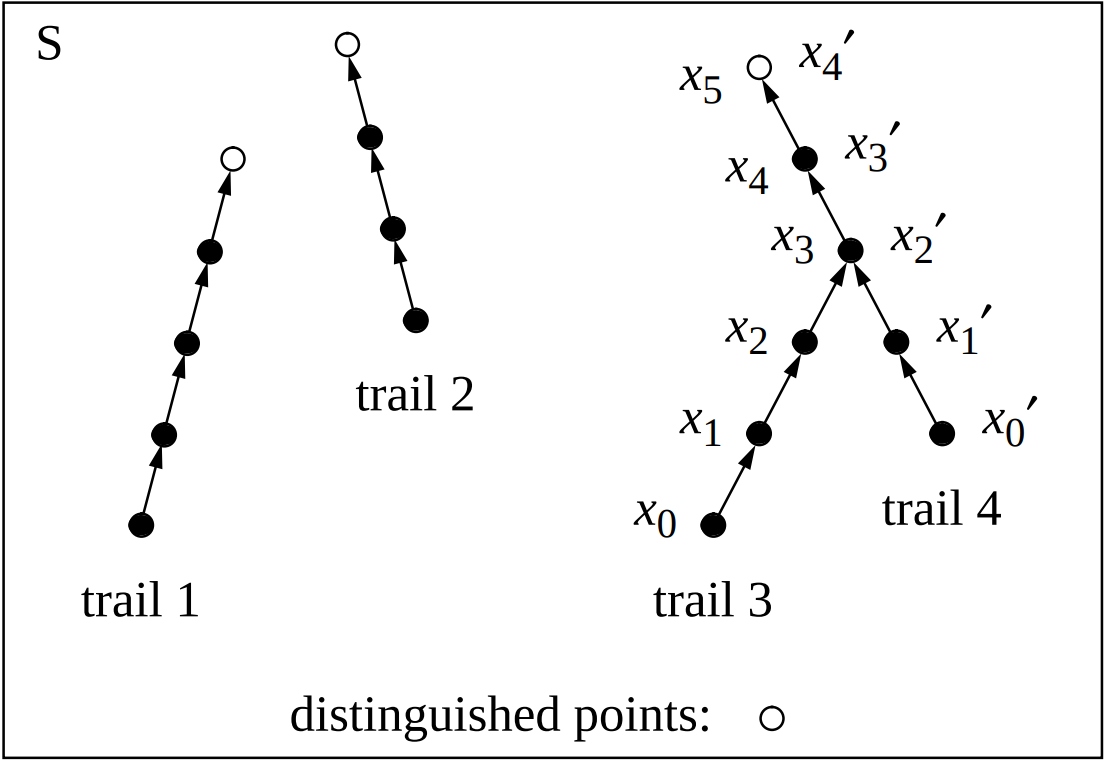
Figure: Parallel collision search (credits: [vOW99])

Each parallel thread chooses a random value and sequentially applies the hash function, until a distinguished point is found. This point is then added to the database, together with the starting point. Once a collision in the distinguished points appears in the database, a collision of the hash function can be recovered with overwhelming probability. For an example see collision of Trail 3 and Trail 4 on the figure.

The overhead is proportional to the average trail length, which is equal to $2^l$, where $l$ is the number of zero bits chosen for distinguished points. For all challenges I used $l=25$. The hash size is approximately 91 bits, so we expect to evaluate the hash function $\sqrt{\pi 2^{91}/2}\approx 2^{45.8}$ times before a collision is found. This corresponds to $2^{20.8}\approx 1.9$ million distinguished points. Storing such amount of points requires just small amounts of memory/storage.

The computations were performed on the HPC cluster of the University of Luxembourg [VBCG14], using about 1000 cores. Each solved instance required about 1k-2k core-days of computations. In retrospect, I suppose that using GPUs instead could save lots of computational effort, though I am not sure if it is easy to efficiently implement such arithmetics for GPUs.

Optimizing Arithmetic

All the prime-based targets (with 45-bit security) operate in the finite field $\F_p$ with $p= 2^{91} + 5\cdot 2^{64} + 1$. It is crucial therefore to optimize arithmetic operations over this field. The common operations used are:

addition modulo $p$;
multiplication by a constant modulo $p$;
raising to a power $e$ modulo $p$, typically $e=3$ (cube) or $e=p-2$ (inversion).

To avoid much of a hassle, I used __uint128_t type as a basis, available in many compilers. The addition is straightforward:

__uint128_t add(__uint128_t a, __uint128_t b) {
    __uint128_t res = a + b;
    return (res >= MOD) ? (res - MOD) : res;
}

Optimizing Modular Reduction

However, multiplication is more tricky. The product of two 91-bit numbers can easily overflow 128-bit type. This issue can be solved by splitting one of the operands into 32-bit chunks, multiplying them separately and summing the result. Intermediate values then should be reduced modulo $p$ to prevent overflow. Generally speaking, modulo reduction is a very heavy operation. Luckily, the selected prime $p$ has a special form, which allows to avoid any integer division. This is done by performing divisions by powers of 2, which are implemented as simple binary shifts.

We need to implement multiplication by $2^{32}$ and multiplication by a 32-bit number (with immediate reduction modulo $p$). Both can be implemented using one tool: reduction of a 125-bit value $a$ modulo $p$ (note that values of $\F_p$ in general require 92 bits and $2^{32}$ is a 33-bit value). Let $t = \floor{a / p}$ and note that $t < 2^{125}/p < 2^{34}$. For some $\eps \le p$ $$ a = 2^{91}t + 5\cdot 2^{64}t + \eps. $$ Observe that $\tilde{t} := \floor{a / 2^{91}}$ is almost equal to $t$: $$ \tilde{t} = \floor{a / 2^{91}} = t + \floor{ \frac{(5\cdot 2^{64}t + \eps)}{2^{91}} } \le t + 2^{101}/2^{91} = t + 2^{10}. $$ Let's subtract $\tilde{t}p$ from $a$. In order to be safe from possible extra $2^{10}$ multiplies of $p$, we can add $2^{10}p$ to the result. Let $$a' := a - \tilde{t}p + 2^{10}p.$$ We know that $0 \le a' \le 2^{10}p$. Let's repeat the procedure! We now have that $$t' := \floor{a' / p} \le 2^{10},~\text{and}$$ $$\tilde{t'} := \floor{a' / 2^{91}} = t' + \floor{ \frac{(5\cdot 2^{64}t' + \eps')}{2^{91}} } \le t' + 1.$$ That is, after the second step the "underflow" is at most by one $p$, which can be eliminated using a single if.

The final step is to get rid of 128-bit multiplications in the computation of $a'$ given by $a' = a - \tilde{t}p + 2^{10}p$. Here we can split $p$ into two 64-bit words and compute separately the highest and the lowest word to be subtracted from $a$.

The whole reduction step can be implemented as follows (note that 5*t can be further optimized as (t<<2)+t, and it seems to be done by compilers):

#define EXP2(i) (E<<(i))
const __uint128_t E = 1;

const __uint128_t MOD = EXP2(91) + 5*EXP2(64) + 1;
const __uint128_t MODMASK = EXP2(91) - 1;
const __uint128_t MODe10 = MOD << 10;

__uint128_t reduce(__uint128_t a) {
    uint64_t t = (a >> 91);
    a &= MODMASK;
    a += MODe10;
    a -= ((__uint128_t)(5*t)<<64) + t;
    uint64_t tt = (a >> 91);
    a &= MODMASK;
    a += MOD;
    a -= ((__uint128_t)(5*tt)<<64) + tt;
    if (a >= MOD) a -= MOD;
    return a;
}

Optimizing Multiplication

Let's get back to the 32-bit chunk multiplication idea. Assume we want to multiply $a,b \in \F_p$. Let $b_0,b_1,b_2 < 2^{32}$ be such that $$ b = 2^{64}b_2 + 2^{32}b_1 + b_0.$$ Then $$a\cdot b = a \cdot b_0 + (2^{32}a) \cdot b_1 + (2^{64}a) \cdot b_2.$$ This is nicely implemented by the following code:

__uint128_t multiply(__uint128_t a, __uint128_t b) {
    __uint128_t res = 0;

    res += a * (uint32_t)b;
    b >>= 32;
    a = reduce(a << 32);

    res += a * (uint32_t)b;
    b >>= 32;
    a = reduce(a << 32);

    res += a * (uint32_t)b;
    return reduce(res);
}

Optimizing Cube Mapping

The cube mapping is rather straightforward: $a^3 = (a\cdot a) \cdot a$. However, there is a little optimization here as well. Observe that in the multiplication we compute reduced $a, 2^{32}a, 2^{64}a$. Since in the cube mapping we multiply by $a$ two times, we can reuse these values between the two multiplications:

__uint128_t cube(__uint128_t a) {
    __uint128_t a1 = a;
    __uint128_t a2 = reduce(a1 << 32);
    __uint128_t a3 = reduce(a2 << 32);

    __uint128_t res = 0;
    res += a1 * (uint32_t)a; a >>= 32;
    res += a2 * (uint32_t)a; a >>= 32;
    res += a3 * (uint32_t)a;
    a = reduce(res);

    res = 0;
    res += a1 * (uint32_t)a; a >>= 32;
    res += a2 * (uint32_t)a; a >>= 32;
    res += a3 * (uint32_t)a;
    return reduce(res);
}

Concrete Instances

GMiMC-erf (Small)

GMiMC-erf is a generalized Feistel Network with expanding round function (thus, "erf"). The cube mapping is applied to one of the branches and the result is added to all other branches. After this simple step, the branches are rotated to the left by one position.

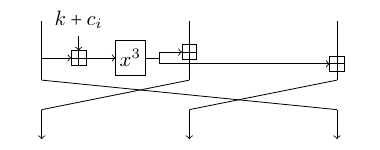
Figure: Single Round of GMiMC-erf with 3 Branches

Remark: GMiMC is a block cipher. However, the key is not used as only a permutation is needed.

The small instance proposed at the STARK-Friendly Hash Challenge has 3 branches taking values over $\F_p$. The rate is 2 branches and the capacity is only 1 branch. The number of rounds is 121.

Since there is nothing special here, the optimized arithmetic described above is probably the largest chunk of what can be optimized, so I did no further optimizations.

With this instance I was very lucky and got a collision already after 0.7M distinguished points (out of 1.8M expected). The collision is:

m1 = [0x27595c22ac533626fbe205f, 0]
m2 = [0x27cd95ff999a21991a8d46c, 0]

GMiMC-erf (Large)

The larger variant of GMiMC-erf differs only in the number of branches: it has 11 branches! 10 of which are rate, and 1 is the capacity. The number of rounds is slightly increased up to 137 rounds.

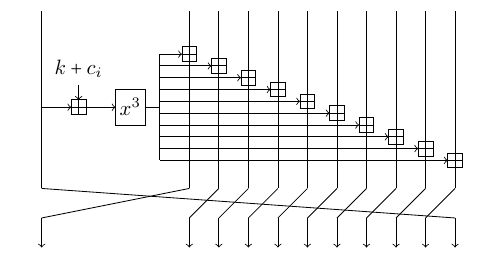
Figure: Single Round of GMiMC-erf with 11 Branches

Since the increased number of branches only increases the number of additions in the field, the overhead should not be very large. The cube function is still the dominating part. Nonetheless, there is a nice trick to save a fraction of the time. In fact, the trick allows to compute a round of GMiMC-erf with arbitrary amount of branches at the same cost as for 4 branches (more precisely, with 2 additions and 1 subtraction).

The idea is to note that the same value is added to all branches. This addition can be postponed. Let's keep an extra value such that the actual correct state is recovered from the current state by adding the extra value to each branch. Initially, we set this value to 0 to satisfy the invariant. After the last round, the recovery procedure is performed. Since the number of rounds is large, the procedure cost is negligible. This leads to the following equivalent structure:

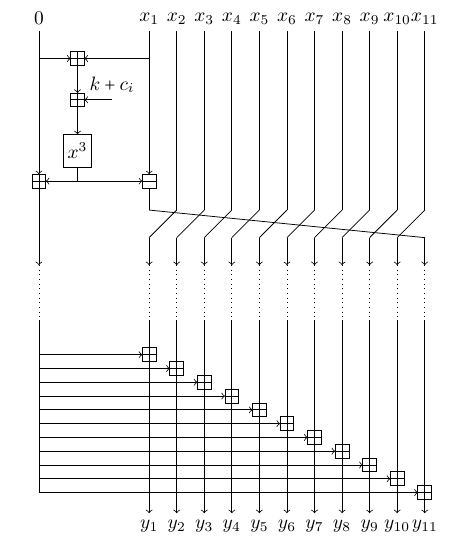
Figure: Optimized Structure of GMiMC-erf with 11 Branches

Finally, the rotations may be postponed as well. This leads to the following C code:

const int NROUNDS = 137;
const int NWORDS = 11;
void permutation(F *state) {
    F sum;
    int k = 0;
    for(int i = 0; i < NROUNDS; i++) {
        state[k] = state[k] + sum;
        sum = sum + (state[k] + CONST[i]).cube();
        state[k] = state[k] - sum;
        k++;
        if (k >= NWORDS) k = 0;
    }
    // k rotations
    for(; k > 0; k--) {
        for(int j = 1; j < NWORDS; j++) {
            swap(state[j-1], state[j]);
        }
    }
    // flush sum
    for(int j = 0; j < NWORDS; j++) {
        state[j] = state[j] + sum;
    }
    return;
}

With this instance the collision was obtained after 1.1M distinguished points (out of 1.8M expected). The collision is:

m1 = [0x762c86fa8d8df1fa8b7ef48, 0, 0, 0, 0, 0, 0, 0, 0, 0]
m2 = [0x45d71aa5850359d8e302634, 0, 0, 0, 0, 0, 0, 0, 0, 0]

Poseidon (Small)

The Poseidon block cipher / permutation has a different structure: substitution-permutation network (SPN). The S-Box is the cube function over $\F_p$ and the linear layer is an MDS matrix over $\F_p$. Poseidon is special in that it uses only 1 S-Box in the middle rounds. This allows to counter algebraic/interpolation attacks using the same number of rounds as a full SPN, while making the cipher much lighter. Similarly to GMiMC, at the competition the 91-bit Poseidon comes with $m=3$ and $m=11$ branches.

The MDS matrix multiplication can be slightly boosted using the following trick. The computation consists in multiplying the input words by values in the matrix and summing the results. Since the matrix is fixed, only multiplications by constansts are performed. Recall the multiplication method for $a,b \in \F_p$: $$a\cdot b = a \cdot b_0 + (2^{32}a) \cdot b_1 + (2^{64}a) \cdot b_2.$$ If $a$ is the constant and $b$ is an input word, we can precompute and store values $a, 2^{32}a, 2^{64}a$ modulo $p$ for each constant $a$ in the MDS matrix. This allows to save some calls to the reduction routing.

During execution of the attack, I accidentally used 90 bits of the output instead of 91. As a result, a 90-bit collision was found. As the extra bit could match with probability 1/2, I continued the search. Due to bad luck, the full 91-bit collision appeared only after 7 90-bit collisions! As a result of this little error, 3.5M points were computed in total. The final collision is:

m1 = [0x3a327029e5b4c8dd7bf671c, 0]
m2 = [0x13502e7e69859c4f9e34d9d, 0]

Acknowledgements

This work was supported by the Luxembourg National Research Fund (FNR) project FinCrypt (C17/IS/11684537). The experiments presented in this work were carried out using the HPC facilities of the University of Luxembourg [VBCG14] -- see hpc.uni.lu.